
Numerische und Relativistische Astrophysik
Numerische Relativitätstheorie
Um zu verstehen, wie sich Schwarze Löcher und Neutronensterne bilden und was passiert, wenn diese miteinander verschmelzen, müssen wir einerseits die Einstein-Gleichungen vollständig lösen, und sowohl die Bewegungsgleichungen für Materie und elektromagnetische Felder als auch Strahlungstransfergleichungen in der Allgemeinen Relativitätstheorie. Es ist im Allgemeinen nicht möglich, diese nichtlinearen partiellen Differentialgleichungen analytisch zu lösen. Daher benutzen wir stattdessen numerische Simulationen auf Hochleistungscomputern, für die wir seit den 1990er Jahren neue Methoden der numerischen Relativitätstheorie entwickeln. Mittels computerunterstützter numerischer Methoden ist es außerdem möglich, genaue Lösungen für Gleichungen der Hydrodynamik/Magnetohydrodynamik zu finden sowie Näherungslösungen der Strahlungshydrodynamik-Gleichungen für den Neutrinotransport.
Wir untersuchen derzeit eine Vielzahl dynamischer und allgemein-relativistischer Phänomene wie beispielsweise
- die Verschmelzung von Doppelsystemen aus Neutronensternen oder aus Schwarzen Löchern und Neutronensternen,
- den Kollaps von Sternen zu einem Schwarzen Loch und einem umgebenden Materietorus,
- die Bildung eines extrem massereichen Schwarzen Lochs durch den Kollaps eines sehr massereichen Sterns,
- die Entwicklung von Schwarzen Löchern und Neutronensternen durch die Akkretion von Materie,
- Materieausfluss und Jets von Schwarzen Löchern und Neutronensternen.
Diese Simulationen im Rahmen der Allgemeinen Relativitätstheorie spiele eine wichtige Rolle bei der Vorhersage von Wellenformen, die für den Nachweis von Gravitationswellen benötigt werden, und für den Nachweis von hochenergetischen Phänomenen wie den Gammablitzen. Numerische Relativität ist außerdem wichtig, um die nichtlinearen Eigenschaften von Theorien der Gravitation zu erforschen.
Vorhersage von Gravitationswellenformen
Gravitationswellen werden durch allgemein-relativistische und dynamische Phänomene erzeugt, wenn das System nicht kugelsymmetrisch ist. Wenn starke Gravitationswellen erzeugt werden, können sie mit Gravitationswellen-Detektoren wie Advanced LIGO und Advanced Virgo nachgewiesen werden und zukünftig auch mit KAGRA und LISA, dem Gravitationswellen-Detektor im All. Die Advanced LIGO- und Virgo-Detektoren haben bereits Gravitationswellen von Doppelsystemen Schwarzer Löcher und Neutronensternen nachgewiesen.
Wir erwarten, dass die Detektoren in nächster Zukunft viele Quellen von Gravitationswellen beobachten. Nach der Beobachtung müssen wir die Quelle identifizieren und Informationen wie Masse, Eigendrehung (Spin) und Entfernung aus den Daten extrahieren. Dafür müssen wir „Schablonen“ für die Gravitationswellen berechnen, die von den erwarteten Quellen abgestrahlt werden. Wir führen derzeit eine große Anzahl numerisch-relativistischer Simulationen durch: für die Verschmelzung von Doppelsystemen aus Neutronensternen und Doppelsystemen aus Schwarzen Löchern und Neutronensternen, für den Kollaps von Sternen zu einem sternengroßen und extrem massereichen Schwarzen Loch usw. Dabei wollen wir die entsprechenden Gravitationswellenformen möglichst präzise vorhersagen.
Neutronensternverschmelzungen
Die Verschmelzung eines Doppelsystems aus Neutronensternen ist eine der vielversprechendsten Quellen für Gravitationswellen-Detektoren wie Advanced LIGO, Advanced Virgo, KAGRA sowie für kurze und harte Gammablitze. Um die bei der Verschmelzung von Doppelneutronensternsystemen erzeugten Gravitationswellenformen vorhersagen zu können und um die Verschmelzungshypothese der kurzen und harten Gammablitze zu untersuchen, ist die numerische Relativitätstheorie der geeignete Ansatz. Darüber hinaus wird die Verschmelzung von Doppelsystemen aus Neutronensternen und der damit verbundene Prozess des Massenauswurfs als hauptsächliche Umgebung für Nukleosynthese im r-Prozess vorgeschlagen. Um diese Hypothese zu untersuchen, ist die numerische Relativität wieder der geeignete theoretische Ansatz. Wir haben an diesem Problem die letzten zwei Jahrzehnte hindurch gearbeitet und viel über den Verschmelzungsprozess und die Gravitationswellenformen herausgefunden.
Verschmelzung von Doppelsystemen aus einem Schwarzen Loch und einem
Neutronenstern
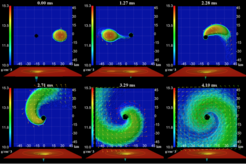
Auch die Verschmelzung von Doppelsystemen aus Schwarzen Löchern und Neutronensternen stellt eine wichtigste Quelle von Gravitationswellen dar und gilt auch als vielversprechender Kandidat für den zentralen Motor kurzer und harter Gammablitze. Für solche Systeme gibt es, allgemein gesagt, zwei mögliche Entwicklungen. In dem einen Szenario wird der Neutronenstern einfach von dem Schwarzen Loch verschluckt, in dem anderen wird der Neutronenstern während der Verschmelzung von den Gezeitenkräften zerrissen. Im letzteren Fall erwarten wir viele hochenergetische Phänomenen, inklusive Gammablitze und dem Auswurf von Materie, was zu vorübergehender elektromagnetischen Abstrahlung führt. Diese Phänomene untersuchen wir mittels numerischen Relativität.
Verschmelzung eines Schwarzen Lochs geringer Masse mit einem Neutronenstern
Gravitationskollaps zum Schwarzen Loch
Schwere Sterne entwickeln sich durch eine Reihe von nuklearen Brennprozessen, bis sich in ihrem Zentrum ein Eisenkern gebildet hat. Wenn die Masse des Eisenkerns (und die der umgebenden Schichten) groß genug ist, wird nach dem Kollaps ein Schwarzes Loch entstehen. Wahrscheinlich haben sich durch einen solchen Prozess die massereichen Schwarzen Löcher, die in Doppelsystemen von Advanced LIGO und Advanced Virgo entdeckt wurden, gebildet. Allerdings hat man den Prozess, in dem diese Schwarzen Löcher entstehen, noch nicht gut verstanden.
Jüngste Beobachtungen haben gezeigt, dass Zentren großer Galaxien ein extrem massereiches Schwarzes Loch von einer Million bis zu 10 Milliarden Sonnenmassen enthalten. Jedoch ist der Entstehungsprozess dieser Schwarzen Löcher immer noch unbekannt und gehört zu den seit langer Zeit unbeantworteten Fragen der Astrophysik.
Wir untersuchen diese Probleme im Rahmen der numerischen Relativitätstheorie. Insbesondere führen wir eine Vielfalt von numerisch-relativistischen Simulationen durch – mit verschiedenen plausiblen Ausgangssternen und mit dem Ziel, den Entstehungsprozess Schwarzer Löcher aufzuklären. Dabei erforschen wir die möglichen Signale wie z.B. Gravitationswellen, Neutrinos und elektromagnetische Wellen, die bei zukünftigen Beobachtungen auftreten könnten, die den Entstehungsprozess Schwarzer Löcher aufklären sollen.
Magnetohydrodynamische Simulationen in der Allgemeinen Relativitätstheorie

Magnetische Felder sind bei einer Vielzahl von Phänomenen von großer Bedeutung. Es ist gut möglich, dass Magnetfeldinstabilitäten eine wichtige Rolle bei der Verschmelzung von Doppelneutronensternen und der Entstehung von Massescheiben spielen, die kompakte Objekte umgeben. So wird z.B. während des Zusammenstoßes zweier Neutronensterne unvermeidlich auf der Kontaktfläche der Neutronensterne eine Scherungsschicht gebildet. Es ist bekannt, daß sich auf solch einer Scherungsoberfläche die Kelvin-Helmholtz-Instabilität ausbildet und eine Reihe kleiner Wirbel erzeugt werden. Daraufhin vergrößert die Bewegung der Wirbel die Magnetfeldstärke durch die Verdrillung des Magnetfeldes. Nach der merklichen Verstärkung des Magnetfeldes bilden sich Turbulenzen aus, und die sich daraus ergebende turbulente Viskosität könnte die Entwicklung des Überrests der Verschmelzung bestimmen, weil sie zum Drehimpuls und zur viskosen Erhitzung beiträgt. Um diese Prozesse zu verstehen, führen wir magnetohydrodynamische Simulationen in der Allgemeinen Relativitätstheorie durch. Für eine präzise Untersuchung müssen wir die Kelvin-Helmholtz-Instabilität in der Simulation korrekt berücksichtigen. Dies ist jedoch computertechnisch keine leichte Aufgabe, weil die Kelvin-Helmholtz-Instabilität sich auf sehr kleinen Skalen abspielt, und wir solche kleinen Skalen in der numerischen Relativitätstheorie auflösen müssen. Bis jetzt hat das noch keine Simulation gelöst und daher wurde bisher keine physikalische Simulation durchgeführt. In Zukunft beabsichtigen wir eine extrem hochaufgelöste Simulation durchzuführen, um den Verschmelzungsprozess eines Doppelsystems aus Neutronensternen endgültig aufzuklären. Magnetfeldinstabilitäten könnten auch eine entscheidende Rolle bei der Entwicklung des Überrests des Verschmelzungsprozesses spielen und bei der Bildung der Akkretionsscheibe, die kompakte Sterne umgibt. Es gibt noch viele Aufgaben, die mit Hilfe einer magnetohydrodynamischen Simulation in der Allgemeinen Relativitätstheorie in Angriff genommen werden sollten.
Viskose Hydrodynamik
Eine phänomenologische Möglichkeit, Drehimpulstransport und turbulente Viskosität zu berücksichtigen, ist der Einsatz der viskosen Hydrodynamik. Damit untersuchen wir den Verschmelzungsrest von Doppelneutronensternen und die Akkretionsscheiben, die die zentralen kompakten Objekte umgeben.
Doppelneutronensternsysteme in Skalar-Tensor-Theorien
Bis jetzt gibt es keine Hinweise darauf, dass Beobachtungen nicht mit der Allgemeinen Relativitätstheorie übereinstimmen. Die Tests der Allgemeinen Relativitätstheorie wurden jedoch immer in relativ schwachen Feldern durchgeführt, wie beispielsweise im Sonnensystem oder in Doppelneutronensternsystemen mit großem gegenseitigem Abstand. Da inzwischen Gravitationswellen von verschmelzenden Neutronensternen nachgewiesen wurden, haben wir die große Chance, die Allgemeine Relativitätstheorie in starken Feldern zu überprüfen. Für diesen Test ist es entscheidend, vorherzusagen, was in starken Feldern in einer alternativen Gravitationstheorie geschieht. So haben wir für eine Untersuchung Simulationen der Verschmelzung von Doppelneutronensternen in Skalar-Tensor-Theorien der Gravitation durchgeführt.






