Gravitativer Kollaps
Gravitativer Kollaps zu einem rotierenden Schwarzen Loch
Horizonte
Diese Visualisierung einer Computersimulation zeigt den gravitativen Kollaps eines Neutronensterns zu einem rotierenden Schwarzen Loch. Ein solcher Kollaps ist eine der stärksten Quellen elektromagnetischer und gravitativer Strahlung. Aber nur ein Millionstel der Systemenergie wird in Form von Gravitationswellen abgestrahlt, daher müssen die Berechnungen sehr genau sein, und das numerische Problem ist recht anspruchsvoll. Um gute Vorhersagen über mögliche Gravitationswellensignale machen zu können, muss die Simulation zudem auf einem großen räumlichen Gebiet durchgeführt werden, da die Gravitationswellen ihre so genannte asymptotische Form - wie wir sie auf der Erde nachweisen können - erst weit entfernt von der Quelle annehmen. Mit dem hier verwendeten numerischen Verfahren war es erstmals möglich, die Gravitationsstrahlung eines solchen Ereignisses mit einer vollständig dreidimensionalen Simulation zu berechnen.
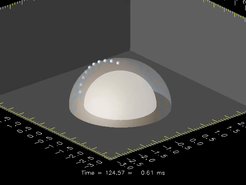
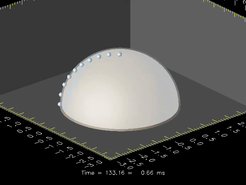
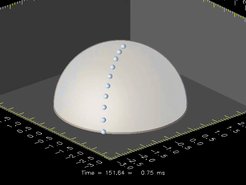
Die Bilder zeigen die Entwicklung des Ereignishorizonts und des scheinbaren Horizonts des Schwarzen Lochs, das durch den Kollaps entstanden ist. Die graue Hemisphäre ist der Ereignishorizont, der die "Oberfläche" des Schwarzen Lochs darstellt. Nichts, nicht einmal Licht, kann aus dem Inneren des Ereignishorizonts entweichen. Mit den kleinen Testvolumina können die Masse und der Spin des Schwarzen Lochs - seine grundlegenden Eigenschaften - bestimmt werden.
Bald nach der Bildung des Ereignishorizonts erscheint der scheinbare Horizont (hellgrau). Dies ist - in einem bestimmten Zeitschritt - die Grenze zwischen Regionen, in denen austretende Lichtstrahlen noch bis ins Unendliche entweichen können und wo sie im Schwarzen Loch gefangen sind. Aber ein Lichtstrahl, der zu einer bestimmten Zeit entkommt, kann an einem späteren Zeitpunkt eingefangen werden, wenn mehr Materie in das Schwarze Loch gefallen ist. Der Ereignishorizont ist dagegen unabhängig vom Zeitpunkt und vom Beobachter: Er trennt die letzten Lichtstrahlen, die jemals aus dem Inneren des Schwarzen Lochs austreten werden. Der scheinbare Horizont befindet sich also immer innerhalb des Ereignishorizonts, bis sie am Ende des dynamischen Entstehungsprozesses zusammenfallen.
Um den Ereignishorizont berechnen zu können, muss die gesamte Entwicklung des Schwarzen Lochs bekannt sein - der scheinbare Horizont kann hingegen während der Entwicklung berechnet werden. Da die Raumregion im Inneren des Horizonts keinen Einfluss auf die Außenregion hat, wurde sie in dieser Simulation ausgeschnitten - auf diese Weise vermeidet man das numerische Problem der Behandlung der Singularität im Inneren des Schwarzen Lochs, wo die Krümmung der Raumzeit unendlich wird.Credits
Bildrechte:
P. Diener (Louisiana State University), L. Baiotti (SISSA), L. Rezzolla (Max-Planck-Institut für Gravitationsphysik & Institut für Theoretische Physik, Frankfurt)
Hinweis: Die Veröffentlichung von Filmen und Bildern bedarf der schriftlichen Einwilligung und erfolgt nur unter Nennung der Rechteinhaber. Bitte kontaktieren Sie aei_zib_images@aei.mpg.de zwecks Einholung der Genehmigung.