Gravitational waveforms with higher modes from merging black holes
The first higher-multipole model of spinning and coalescing black-hole binaries improves accuracy of waveforms and measurement of astrophysical parameters
Together with international colleagues, AEI researchers have for the first time created a higher-multipole model of gravitational waves from binary black holes during inspiral, merger, and ringdown by combining post-Newtonian and pertubation theoretical methods. Their PhenomHM model is an extension of the widely used PhenomD model and is more accurate than the latter for all binary configurations, typically improves the measurement of binary properties, and will also be valuable in strengthening current tests of general relativity.
Paper abstract
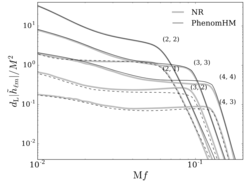
Gravitational-wave observations of binary black holes currently rely on theoretical models that predict the dominant multipoles (l=2, |m|=2) of the radiation during inspiral, merger, and ringdown. We introduce a simple method to include the subdominant multipoles to binary black hole gravitational waveforms, given a frequency-domain model for the dominant multipoles. The amplitude and phase of the original model are appropriately stretched and rescaled using post-Newtonian results (for the inspiral), perturbation theory (for the ringdown), and a smooth transition between the two. No additional tuning to numerical-relativity simulations is required. We apply a variant of this method to the nonprecessing PhenomD model. The result, PhenomHM, constitutes the first higher-multipole model of spinning and coalescing black-hole binaries, and currently includes the (l,|m|)=(2,2),(3,3),(4,4),(2,1),(3,2),(4,3) radiative moments. Comparisons with numerical-relativity waveforms demonstrate that PhenomHM is more accurate than dominant-multipole-only models for all binary configurations, and typically improves the measurement of binary properties.












