Cosmology as a filter for string theory
What determines the shape and properties of extra dimensions? New answers from the Hartle-Hawking no-boundary proposal.
Many observed features of our world remain puzzling – we do not know, for example, why the known particles interact via electric, magnetic, and nuclear forces. String theory has the potential to explain these features by evoking small, additional dimensions. But what determines the shape and properties of these dimensions? In a recent paper, AEI researcher Lehners with his colleagues Leung and Stelle has shown, in a simplified model, that it could be cosmology selecting which solutions are relevant. Using the Hartle-Hawking no-boundary proposal, they demonstrate that certain features of these extra dimensions, for example how much energy they hold, lead to an increased probability for such universes to be created from nothing. By the same token, many solutions become disfavoured because they correspond to universes that have a very small chance of being created. In this way, cosmology can act as a filter on the possible string theory solutions, thereby linking the very large and very small properties of the Universe.
Paper abstract
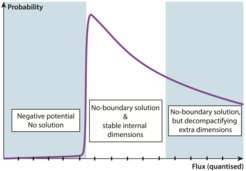
String compactifications typically require fluxes, for example in order to stabilise moduli. Such fluxes, when they thread internal dimensions, are topological in nature and take on quantised values. This poses the puzzle as to how they could arise in the early universe, as they cannot be turned on incrementally. Working with string inspired models in 6 and 8 dimensions, we show that there exist no-boundary solutions in which internal fluxes are present from the creation of the universe onwards. The no-boundary proposal can thus explain the origin of fluxes in a Kaluza-Klein context. In fact, it acts as a selection principle since no-boundary solutions are only found to exist when the fluxes have the right magnitude to lead to an effective potential that is positive and flat enough for accelerated expansion. Within the range of selected fluxes, the no-boundary wave function assigns higher probability to smaller values of flux. Our models illustrate how cosmology can act as a filter on a landscape of possible higher-dimensional solutions.
