Black holes upside down
An AEI Potsdam researcher has investigated, for the first time, energy levels and eigenfunctions of the Schwarzschild black hole quantitatively.
If one were to think about the oscillations of astrophysical systems in terms of musical instruments, the sound of an excited black hole is very short. Black holes are strongly damped systems and rapidly return to a stable and silent configuration. This process reveals a specific sound described in so-called quasinormal modes. Understanding the physical implications of the quasinormal mode spectrum is an active research area. Its scope includes foundational questions about black holes and their gravitational-wave observations. One known theoretical concept is to map these short oscillations to the properties of bound states of an effective system. This mapping turns the problem into one closer to quantum mechanical systems like the Hydrogen atom. In this study an AEI Potsdam researcher shows the first quantitative computation of these bound states for nonrotating black holes. It reveals multiple insights relevant to the original problem and shows that the bound states in the effective system are loosely bound, raising questions about understanding quasinormal modes as local properties close to the black hole. The article also provides complementary insights into open problems related to how robust the properties of the quasinormal modes are to small changes in the black hole system.
Paper abstract
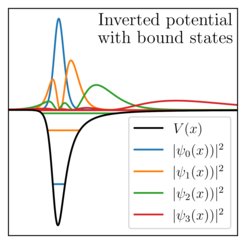
Understanding the physical significance and spectral stability of black hole quasinormal modes is fundamental to high-precision spectroscopy with future gravitational wave detectors. Inspired by Mashhoon’s idea of relating quasinormal modes of black holes with their equivalent bound states in an inverted potential, we investigate, for the first time, energy levels and eigenfunctions of the Schwarzschild black hole quantitatively. While quasinormal modes describe the characteristic damped oscillations of a black hole, the bound states of the inverted potential are qualitatively more similar to those of the hydrogen atom. Although the physical interpretation of these states may initially be of more academic interest, it furthers our understanding of open problems related to quasinormal modes in a similar spirit to Maggiore’s interpretation of the Schwarzschild quasinormal mode spectrum. One surprising insight from the explicit calculation of bound states is that eigenfunctions corresponding to quasinormal mode overtones become rapidly delocalized and extremely loosely bound. This observation raises immediate questions about the common interpretation of quasinormal modes as excitations of the light ring region. Closely related, as a second application, we also explore the spectral stability of bound states and demonstrate that they can provide complementary insights into the quasinormal mode spectrum.
