One ring is a rule to them all
A theorem is proven establishing that, under very generic conditions, any black hole must have a light ring
None of these observations, however, is expected to probe the effective boundary of the black hole, the event horizon. Rather, they should contain a signature of a neighbourhood region slightly outside the horizon, wherein light is bent so strongly it forms closed orbits known as light rings. As a consequence, the properties of these light rings encode much of the relevant black hole properties.
A key question is then: does any black hole model, in any theory of gravity, need to have a light ring?
In this article by P. Cunha and C. Herdeiro, a generic and mathematically innovative argument establishes that an equilibrium black holes must indeed have, as a rule, at least one standard light ring in each rotational sense. The argument is of topological nature and does not use the equations of motion of any theory of gravity, but only regularity requirements, together with horizon and far-away properties.
Indeed, one light ring is a rule to them all.
Paper abstract
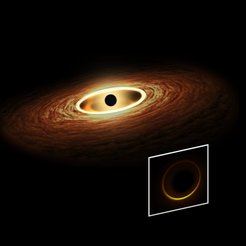
The ringdown and shadow of the astrophysically significant Kerr Black Hole (BH) are both intimately connected to a special set of bound null orbits known as Light Rings (LRs). Does it hold that a generic equilibrium BH must possess such orbits? In this letter we prove the following theorem. A stationary, axi-symmetric, asymptotically flat black hole spacetime in 1+3 dimensions, with a non-extremal, topologically spherical, Killing horizon admits, at least, one standard LR outside the horizon for each rotation sense. The proof relies on a topological argument and assumes C2-smoothness and circularity, but makes no use of the field equations. The argument is also adapted to recover a previous theorem establishing that a horizonless ultra-compact object must admit an even number of non-degenerate LRs, one of which is stable.












