What is complexity in particle physics?
Physicists bridge the gap between two different proposals for complexity in quantum field theories, paving the way towards a better understanding of quantum gravity.
Ideas from quantum information theory have become increasingly relevant in high-energy physics. One such concept is complexity, a quantity which is also important in experimental realizations of quantum computers, describing how difficult it is to perform an operation or task. In quantum field theories, the building blocks of the standard model in particle physics, there have been two different proposals on how complexity can be defined. These are known as circuit complexity, based on an operatorial approach, and path integral optimization, originating from ideas in tensor networks - methods that allow efficient simulations of quantum many-body systems. In the present work, the authors show that the latter one can be understood as a particular choice in the language of circuit complexity. This insight not only allowed the authors to unify these two different concepts, but can also provide a starting point for further quantitative explorations of complexity in quantum field theories and holography, i.e. dual gravitational theories. Interestingly, in the latter context of quantum gravity, complexity might be a probe of black hole interiors and related to the emergence of dynamical spacetimes from microscopic quantum mechanical degrees of freedom, both of which are timely problems in ongoing research.
Paper abstract
Early efforts to understand complexity in field theory have primarily employed a geometric approach based on the concept of circuit complexity in quantum information theory. In a parallel vein, it has been proposed that certain deformations of the Euclidean path integral that prepares a given operator or state may provide an alternative definition, whose connection to the standard notion of complexity is less apparent. In this letter, we bridge the gap between these two proposals in two-dimensional conformal field theories, by explicitly showing how the latter approach from path integral optimization may be given a concrete realization within the standard gate counting framework. In particular, we show that when the background geometry is deformed by a Weyl rescaling, a judicious gate counting allows one to recover the Liouville action as a particular choice within a more general class of cost functions.
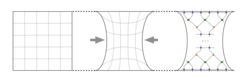
The first panel on the left represents a strip of flat two-dimensional geometry. The straight dashed lines, that make up a grid, represent slices of constant time (horizontal) and constant spatial position (vertical). The middle panel represents a strip of deformed two-dimensional geometry obtained after rescaling the flat geometry on the left. Here, the curved dashed lines also represent slices of constant time (horizontal) and constant spatial position (vertical). The arrows on the sides of the panel show the effect of the rescaling on the geometry. The third panel on the right represents a special type of tensor network called 'euclidean MERA' (Multiscale Entanglement Renormalization Ansatz) which in this case implements the time evolution in the deformed (rescaled) geometry. This tensor network consists of three types of tensors: the green rectangles represent a type of tensor called 'disentangler', the yellow triangles represent 'isometries', and the blue circles represent 'euclideons'.
Research background
Among the most exciting developments in theoretical physics is the confluence of ideas from quantum many-body systems, quantum information theory, and gravitational physics. A natural meeting point for such ideas lies in holographic theories, which are a class of quantum field theories that admit a description in terms of a dual gravitational theory. Holographic theories are a realization of the holographic principle: the idea that all the physical information of a (d+1)-dimensional gravitational theory is encoded in a d-dimensional quantum theory living at the conformal boundary of the spacetime. In this context, it is said that the spacetime "emerges" from the quantum data at the boundary.
Recent progress in this area includes the development of tensor network methods for simulating quantum many-body systems [1], and the elucidation of the role of certain extremal surfaces in the emergence of spacetime in holographic theories [2]. The central technical tool in these ground-breaking results is the reduced density matrix for a spatial subregion and the associated von Neumann entropy, called in this case the entanglement entropy. Broadly speaking, the entanglement entropy measures how much information about the full quantum state is stored in a given spatial subregion.
However, insights from black hole physics suggest that other surfaces may also play an important role in reconstructing the spacetime in holographic theories, since these capture information beyond entanglement entropy. These geometric objects are conjectured to be dual to the “complexity” of the boundary field theory, according to the competing “complexity = volume” (CV) [3] and “complexity = action” (CA) [4] proposals. However in order to make sense of such proposals, a precise definition of complexity in quantum field theory is needed.
The concept of complexity has its origins in quantum information science, an area developed within the framework of quantum mechanics. The general idea behind complexity is to quantify how difficult it is to reach a certain quantum state starting from another one. That is, how "complex" is this final target state compared to the original reference state. In order to quantify this, one considers "quantum circuits" built from a succession of quantum operations that are performed on the original reference state. Given a set of allowed quantum operations, called gates, the complexity of the target state is defined as the number of gates in the optimal circuit that can be built to reach said target state from the reference state. This procedure is usually referred to as "gate counting”, and the measure of complexity obtained in this way is called ‘circuit complexity’. To find this optimal circuit, a "geometrisation" procedure was proposed [5,6], in which quantum circuits are represented by geodesics in an auxiliary manifold whose length measures the ‘depth’ of the circuit associated to them. The complexity of the circuit is then associated with the length of the minimal geodesic whose endpoints represent the reference and target states.
This approach to complexity in quantum mechanics was taken as the basis for an implementation in free quantum field theories [7] with similar results and holographic predicitions to an approach based on the Fubini-Study metric [8]. This proposed field-theoretic definition of circuit complexity has also proven to be useful in studying scaling properties of time-dependent phenomena in free bosonic field theory as well as in providing a viable definition in the case of subregions/mixed quantum states [9]. It has also been studied in the case of the Thermofield Double State (TFD) in order to probe its holographic properties [10].
However, there exists an independent approach to complexity in quantum field theories which has its origins in tensor networks [11]. In this approach, one considers an optimization procedure for Euclidean path-integrals that evaluate field theory wave functionals. The optimization is performed by minimizing certain functional, which is interpreted as a measure of computational complexity, with respect to background metrics for the path-integrals. This functional, called the “path-integral complexity”, describes the size of the path-integration and corresponds to the computational complexity in the equivalent tensor network description. In two dimensional conformal field theories, it turns out that this functional is given by the well-known Liouville action.
From a first glance, these two approaches seem very distinct and provide alternative definitions of complexity in quantum field theories. This is undesirable, as one crucial objective is to make a connection with the proposed dual holographic interpretations of complexity, which requires a precise definition applicable in interacting quantum field theories.
The aim of our most recent work [12] was to bridge the gap between these two approaches by explicitly showing that the second approach, namely the path-integral complexity, can be given a concrete realization in terms of the circuit complexity formalism, in the context of two-dimensional conformal field theories. We did this by showing that it is possible to recover the Liouville action as a circuit complexity measure, and that in fact, it can be thought of as an approximation to a genuine gate counting procedure. This insight not only allows to unify these two different concepts but it also provides a stepping stone for further quantitative explorations of complexity in quantum field theories and holographic theories.
In light of the successes born of entanglement entropy mentioned previously, understanding complexity in quantum field theory represents a very promising research direction to further understand the holographic duality and ultimately information-theoretical aspects of quantum gravity.
References and Further Reading
[1] R. Orus, Ann. Phys. (Amsterdam) 349, 117 (2014).
[2] S. Ryu, and T. Takayanagi, Phys. Rev. Lett. 96, 181602 (2006),
[3] L. Susskind, arXiv:1411.0690 [hep-th],
[4] A. R. Brown, et al., Phys. Rev. Lett. 116, 191301 (2016),
[5] M. Nielsen, arXiv:quant-ph/0502070 (2005),
[6] M. Nielsen, et al., arXiv:quant-ph/0603161 (2006),
[7] R. Jefferson, and R.C. Myers, High Energ. Phys. (2017) 2017: 107,
[8] S. Chapman, M. P. Heller, H. Marrochio, and F. Pastawski,
Phys. Rev. Lett. 120, 121602 (2018),
[9] H. A. Camargo, P. Caputa, D. Das, M. P. Heller, and R. Jefferson,
Phys. Rev. Lett. 122, 081601 (2019),
[10] S. Chapman, J. Eisert, L. Hackl, M. P. Heller, R. Jefferson, H. Marrochio, and
R. C. Myers, SciPost Phys. 6, 034 (2019)
[11] P. Caputa, et al., J. High Energ. Phys. (2017) 2017: 97,
[12] H. A. Camargo, M. P. Heller, R. Jefferson, and J. Knaute,
Phys. Rev. Lett. 123, 011601 (2019).

