Modellierung von Quellen und Astrophysik
Die genaue und effiziente Berechnung der Gravitationswellen-Emission von extremen astrophysikalischen Ereignissen ist der Hauptzweck bei der Modellierung von Quellen. Numerische und analytische Relativitätstheorie treffen aufeinander um Wellenform-Modelle zu berechnen. Solche Modelle haben Experimentalphysiker benutzt, um die Gravitationswellen nachzuweisen und zu charakterisieren, die im ersten Beobachtungslauf von Advanced LIGO beim Zusammenstoß zweier Schwarzer Löcher erzeugt wurden.
Warum werden Quellen modelliert?
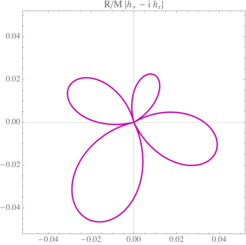
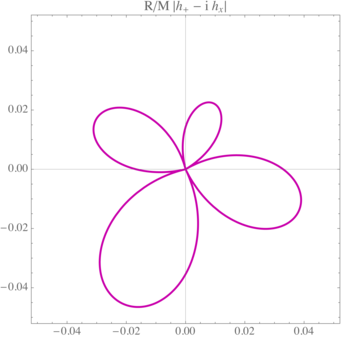
Bei extremen astrophysikalischen Ereignissen, wenn große Massen sich mit nahezu Lichtgeschwindigkeit bewegen, werden charakteristische Gravitationswellensignale erzeugt. Wenn man versucht, Gravitationswellen mit interferometrischen Experimenten nachzuweisen, müssen die Datenanalytiker gegen viele verschiedene Rauschquellen ankämpfen (Umgebung, instrumental, thermisch, ...), die das begehrte Signal verdecken. Idealerweise wüsste man gern, wonach man in den Daten suchen sollte, um Rauschen und Gravitationswellen zu trennen. Das bedeutet, dass man vorhersagt was die plausiblen Gravitationswellenformen astrophysikalischen Ursprungs in dem Frequenzbereich sind, welcher dem experimentellen Aufbau zugänglich ist. Für Frequenzen zwischen 10 und 1000 Hz (der augenblickliche Stand der Technik für Interferometer auf der Erde) sind die lautesten Quellen von Gravitationswellen verschmelzende Binärsysteme aus kompakten Objekten: die LIGO-Virgo-KAGRA-Kollaboration entdeckt seitdem regelmäßig Verschmelzungen von Schwarzen Löchern und/oder Neutronensternen. Diese Systeme stehen im Mittelpunkt des Interesses unserer Abteilung. Die Motivation für diesen Forschungszweig ist ebenfalls theoretischer Natur und besteht darin, die Gleichungen der Allgemeinen Relativitätstheorie in solchen herausfordernden Szenarien zu lösen. Kurz gesagt: das Ziel der Quellenmodellierung besteht darin, die Astrophysik der Quellen von Gravitationswellen in der effektivsten Weise mit den Beobachtungen zu verbinden.
Worin besteht die Gravitationswellen-Signatur von kompakten Binärsystemen?
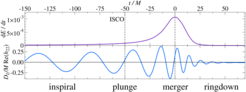
Nach der Allgemeinen Relativitätstheorie senden zwei Objekte, die sich umkreisen, Gravitationswellen aus. Sie machen dabei vier Phasen durch: Während der Umlaufphase verringert sich ihre Kreisbahn, das führt zur Phase des Zusammensturzes und schließlich zur Verschmelzungsphase. Danach kommen sie in einem Überrest zur Ruhe (Abklingphase). Für den höchst dynamischen Bereich in der Nähe der Verschmelzung müssen numerische Simulationen eingesetzt werden, um eine genaue Beschreibung des Systems durch Schablonen für die Detektoren zu erhalten. Das ist für die Detektoren entscheidend, um ihr Nachweispotential zu erreichen und um die Gravitationswellendaten mit den Eigenschaften von Systemen Schwarzer Löcher zu verknüpfen.

Ein großer Teil der Forschung in der Abteilung ist auf die numerische Modellierung von Binärsystemen aus Schwarzen Löchern gerichtet. Diese Simulationen sind rechenintensiv und gegenwärtig nur für eine begrenzte Anzahl von Binärkonfigurationen aus dem gesamten siebendimensionalen Parameterbereich durchführbar, parametrisiert durch das Verhältnis der Massen und der Drehimpulse (Spins) Schwarzer Löcher. Ein besonderer Schwerpunkt liegt auf der Erforschung von Systemen, bei denen die Fehlausrichtung der Spins des Schwarzen Lochs mit dem Bahndrehimpuls die Orbitalebene und die Spins präzedieren lässt. Diese Präzession ist der Gravitationswellenform aufgeprägt, und ein detailliertes Verständnis ihrer Auswirkungen ist wichtig, um ein Maximum an Informationen über Gravitationswellenquellen zu erhalten.
Ein weiterer wichtiger Bereich besteht in dem Ausweiten der Grenzen der Berechenbarkeit, um ein großes Massenverhältnis (> 8), höhere Spins (bis zu dimensionslosen Spins von 0,9) von Binärsysteme mit Dutzenden Umlaufbahnen zu simulieren. Es wird vorausgesagt, dass solche Systeme von astrophysikalischem Interesse sind; sie können als Stellvertreter für Binärsysteme aus Neutronensternen und Schwarzen Löchern dienen.
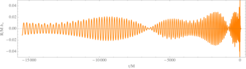
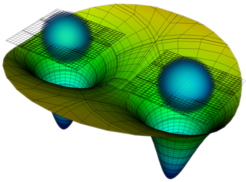
Mitglieder unserer Abteilung haben auch die Verschmelzung von Neutronensternen untersucht, welche die zentrale Quelle für kurze Gammastrahlen-Ausbrüche sind und eine Quelle für die schweren Elemente in unserm Universum. Diese heftigen Ereignisse erzeugen sowohl Gravitationswellen als auch elektromagnetische Strahlung. Innerhalb von Neutronensternen existiert die Materie unter Drücken und Dichten, die in irdischen Laboren nicht herstellbar sind. Deshalb erlauben es Neutronensterne und insbesondere die Zusammenstöße von Neutronensternen, die unbekannte kalte Zustandsgleichung abzuleiten. Die Simulation von Binärsystemen aus Neutronensternen stellt wegen der komplizierten Gleichungen der Materiefelder eine echte Herausforderung dar. Es ist uns jedoch gelungen, lange und genaue Gravitationswellenformen zu simulieren, die Dutzende von Gravitationswellenzyklen anhielten und das über eine großen Bereich des Parameterraums für Neutronensterne. Wir haben sowohl die ersten Simulationen für präzedierende Binärsysteme aus Neutronensternen durchgeführt, als auch Systeme mit dem bislang höchsten Massenverhältnis untersucht. Das gewonnene Wissen hat uns direkt zur Beobachtung und Interpretation des ersten Binärsystems aus Neutronensternen geführt.
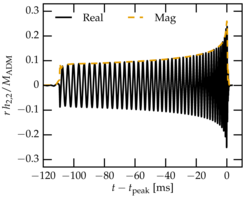
Um Einsteins Gleichungen numerisch zu lösen, muss man sie in einer für die Zeitentwicklung geeigneten Form neu formulieren. Seit dem Durchbruch der Numerischen Relativität im Jahr 2005 wurden mehrere Ansätze entwickelt. Unsere Abteilung nutzt meistens den Spektralen Einstein-Code (SpEC), der von vielen Institutionen gemeinsam entwickelt wurde. SpEC nutzt pseudospektrale Methoden um mit relativ geringem Aufwand eine sehr hohe Genauigkeit zu erreichen. Hochgenaue Simulationen sind unerlässlich, um mit Hilfe der numerischen Relativität Gravitationswellen-Schablonen zu konstruieren, da interferometrische Detektoren sehr genau auf Phasenfehler reagieren, die sich während der Verschmelzung aufaddieren. Wegen der hohen Genauigkeit der spektralen Methoden kann SpEC benutzt werden, um sehr lange numerisch-relativistische Simulationen durchzuführen, die bis zu 100 Gravitationswellen-Zyklen umfassen. Dies erleichtert die Erstellung von sehr langen Schablonen, wie sie für moderne Detektoren und die Kalibrierung und das Studium halbanalytischer Näherungen benötigt werden.
Mitglieder unserer Abteilung verfügen auch über das nötige Fachwissen und haben an der Entwicklung anderer numerischer Codes mitgewirkt (am wichtigsten sind hier BAM und das Einstein Toolkit). Diese Codes wurden ebenfalls sehr erfolgreich beim Studium der Verschmelzung kompakter Binärsysteme eingesetzt. Beide Codes benutzen finite Differenzen, um die Raumzeit zu zerlegen, was Flexibilität und Robustheit bei der Anwendung auf eine Vielzahl von Systemen bietet und die Untersuchungen mit SpEC ergänzt.
Wie begegnet unsere Abteilung den Forderungen der Datenanalytiker?
Die Anzahl möglicher Binärsysteme ist sehr groß, so dass ein rein numerisch-relativistischer Ansatz weder machbar noch praktikabel ist. Um die Sache noch schwieriger zu machen: Wellenformen müssen in derart kurzer Zeit generiert werden, die um Größenordnungen unter dem liegt, was heute für numerisch-relativistische Codes möglich ist.
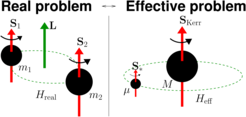
Unsere Abteilung arbeitet an der Herstellung von halb-analytischen Modellen, die mit geringem Aufwand lösbar sind, aber trotzdem genaue Vorhersagen der Wellenformen liefern. Ein sehr erfolgreicher Ansatz, der unter der Bezeichnung effektives Ein-Teilchen-Modell läuft, startet mit einer Erweiterung der Allgemeinen Relativitätstheorie durch eine Störungsrechnung, d.h. im Rahmen der sowohl Post-Newtonschen als auch der Schwarz-Loch-Störungstheorie. Sie zielt auf eine Überbrückung der jeweiligen Geltungsbereiche durch einen einheitlichen Formalismus. In diesem Modell bildet man die Dynamik eines Binärsystems aus Schwarzen Löchern auf die Bewegung einer Testmasse in einem effektiven Raumzeit-Hintergrund ab. Die effektive Raumzeit ist eine Deformation der Kerr-Lösung, die ein rotierendes Schwarzes Loch beschreibt. Die Deformation ist proportional zum Verhältnis der realen Massen des Binärsystems. Die dissipative Dynamik ergibt sich aus geeigneten Summierungen der Post-Newtonschen Formeln für die Gravitationswellenformen. Dieses Modell beruht auf einem Satz gewöhnlicher Differentialgleichungen, die im Vergleich zur umfassenden Allgemeinen Relativitätstheorie schnell zu lösen sind. Und es kann auf numerisch-relativistische Simulationen abgestimmt werden, um seine Vorhersagen zu verbessern.
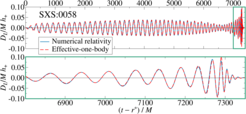
Das Modell wurde durch hunderte von Vergleichen mit der numerischen Relativität bestätigt, die sowohl die konservative Dynamik als auch die Strahlung betreffen. Einen Höhepunkt stellt die Konstruktion eines hochgenauen Modells für Binärsysteme aus Schwarzen Löchern mit generischen Spins dar, die eine generische Präzession durchlaufen können. Dieses Phänomen ist für die extrem komplizierten Gravitationswellensignale verantwortlich, aber die große Komplikation gleicht sich durch den Reichtum an Informationen über die Quelle aus, die in der Wellenform steckt. Dank der führenden Rolle, die wir in der LIGO-Kollaboration spielen, sind die von uns entwickelten Modelle ein Hauptwerkzeug für die LIGO-Datenanalyse. Insbesondere das von unserer Abteilung entwickelte Binärmodell Schwarzer Löcher, die nicht rotieren, wurde benutzt, um die Schablonen zu liefern, welche die Signifikanz der ersten Gravitationswellen-Beobachtungen in den ersten Beobachtungsläufen von Advanced LIGO bestätigten. Unsere Modelle (sowohl mit ausgerichteten Spins als auch mit präzedierenden Spins) wurden auch für die Abschätzung der Parameter von kürzlichen Ereignissen benutzt. Unsere Modelle werden aktiv genutzt beim Nachweis der Verschmelzung kompakter Binärsysteme und der Parameterabschätzung während der Beobachtungsläufe von Advanced LIGO und Virgo.
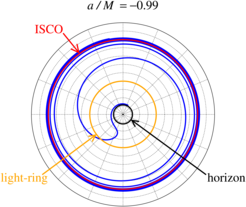
In Zusammenarbeit mit Forschenden anderer Institutionen erforschen wir auch die Störungstheorie Schwarzer Löcher, um die Verschmelzung von Binärsystemen Schwarzer Löcher mit extremen Massenverhältnissen zu studieren (d.h. wenn eines der Schwarzen Löcher deutlich mehr Masse besitzt als sein Begleiter). Das Hauptziel dieser Untersuchungen ist es, das Verhalten von Teilchen, die in rotierende Schwarze Löcher fallen, zu verstehen. Solche Ergebnisse können in effektive Ein-Teilchen-Modelle von entsprechenden Doppelsystemen Schwarzer Löcher eingebunden werden, um das Limit ihres korrekten Massenverhältnisses zu bestimmen. Vollständig relativistische Phänomene (wie etwa quasinormale Modenmischung) können mit Leichtigkeit für eine große Anzahl von Konfigurationen durch die numerische Lösung der Störungsgleichungen erforscht werden.
Wenn eines der beiden kompakten Objekte in einem Doppelsystem ein Neutronenstern ist, so eröffnet sich ein völlig neuer Bereich von möglichen physikalischen Prozessen, dank der Anwesenheit von hochdichter Materie in der Quelle. Dies führt zu einer reichhaltigen Phänomenologie von Wellenformen, die es uns erlaubt, die Eigenschaften von Neutronenstern-Materie zu untersuchen. Mitglieder unserer Abteilung haben unsere Binärmodelle schwarzer Löcher auf Fälle mit Neutronensternen erweitert. Gezeiten- und Resonanzeffekte von Neutronensternen werden erforscht und mit numerisch-relativistischen Simulationen verglichen.
Astrophysikalische Aspekte der Modellierung von Quellen
Von einem astrophysikalischen Standpunkt aus studieren wir Gravitationswellenquellen aller Größen, von Sternenmassen bis zu supermassiven Sternen. Binärsysteme mit stellaren Massen sind mit den heutigen irdischen Detektoren LIGO und Virgo nachweisbar; wir nutzen die relativistische Dynamik zum Studium ihrer Eigenschaften und Häufigkeiten. Wenn Cluster Schwarze Löcher mit mittleren Massen enthalten (mit Massen zwischen hundert und hunderttausend Sonnenmassen) können sie eine starke Quelle von Gravitationswellen sein, wenn sie verschmelzen; sie können mit aLIGO/Virgo beobachtet werden sowie in einigen zehn Jahren mit LISA. Das stellt eine sehr spannende Möglichkeit betreffs der Synergie zwischen zwei Observatorien dar, und mit diesem Punkt haben wir uns in den letzten Jahren befasst. Ein kleines Schwarzes Loch mit der Masse eines Sterns, das um ein supermassives Schwarzes Loch kreist, ist eine der interessantesten Quellen, die wir mit dem geplanten Laser-Interferometer im All (LISA) zu entdecken hoffen. Es hat sowohl das Potential, die Astrophysik von Galaxienzentren und ihrer Schwarzen Löcher aufzuklären als auch die Allgemeine Relativitätstheorie im Bereich starker Felder zu testen. Wir studieren auch das Schicksal von Doppelsystemen Schwarzer Löcher, die sich während der Verschmelzung von Galaxien bilden, insbesondere die Frage, ob die Schwarzen Löcher verschmelzen oder im Abstand unterhalb von einigen Parsec verbleiben. Wir konzentrieren uns auf die Entwicklung in gasreichen Umgebungen in Abständen von einigen Parsec bis hin zum Erreichen der gravitationswellengetriebenen Phase.
Fragen, die durch Quellenmodellierung und Astrophysik behandelt werden:
- Wie sehen Gravitationswellen aus, die von astrophysikalischen Quellen emittiert werden?
- Wie hängen die Wellenformen von der Anwesenheit dichter Materie in den Quellen ab?
- Wie kann man die Wellenformen am schnellsten vorhersagen?
- Wie hängen die Wellenformen von den eigentlichen Parametern der Quelle ab?
- Wie ist der Zusammenhang zwischen der Vereinigung von Galaxien und der Verschmelzung ihrer massiven Schwarzen Löcher?
- Was sind die dynamischen Mechanismen und ihre relativen Gewichte, die EMRIs betreffen? Welche physikalischen Bedingungen herrschen um EMRIs?
- Was ist aus Sicht von Astrophysikern und Kosmologen der größte wissenschaftliche Nutzen bezüglich der Massenfunktionen von SMBHs, IMBHs und die kosmologische Evolution im Zusammenhang mit dem Nachweis von IMRIs?