Observing and Interpreting Gravitational Waves
The Albert Einstein Institute in Potsdam hosts one of the world-leading research groups in searching for gravitational waves from compact-object binaries composed of neutron stars and/or black holes, and inferring astrophysical and physical information upon detection.
Neutron stars and black holes are amongst the most fascinating, and exotic, objects in the Universe. Formed after the death, and subsequent supernova explosion, of massive stars, neutron stars have a mass roughly comparable to our Sun but compressed down into a space roughly equal to that of Berlin. Neutron star matter exists in conditions that are completely impossible to reproduce here on the Earth and therefore the only way that it is possible to probe physics in such extreme regimes is by observing neutron stars in the Universe. Neutron stars have already been observed in our own Galaxy as “pulsars”, which are rotating neutron stars emitting beams of electromagnetic radiation along their magnetic poles. If these beams happen to intersect the Earth as the pulsar spins, we can observe these pulses of electromagnetic emission and therefore the pulsar. While many neutron stars have been observed as pulsars in this way, it is expected that many neutron stars either do not produce such strong electromagnetic emission, or rotate such that the beam does not intersect with the Earth, and therefore remain unobserved.
There is a limit to how massive a neutron star can be – somewhere between 2 and 3.2 times the mass of our Sun – before it is simply too massive to support itself and will collapse further, probably into a black hole. Black holes are dense enough that they warp spacetime so much that even light is unable to escape to be observed by a distant observer. This presents a problem for trying to observe black holes with conventional electromagnetic telescopes. Nevertheless, indirect observations of black holes have been made. For example, by watching stars near the centre of our Galaxy it was noticed that they orbit an invisible object over one million times heavier than the Sun, which surely must be a black hole. Additionally, in so-called X-ray binaries we observe stars being pulled apart by unseen companions and, by observing the accretion of material onto the companions, we strongly suspect the presence of black holes.
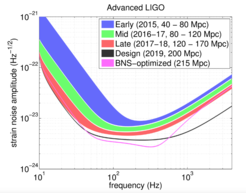
In 2015 the Advanced LIGO observatories directly detected the gravitational-wave signature emitted by merging pairs of black holes hundreds of megaparsecs from the Earth. Advanced LIGO and Advanced Virgo will regularly continue to observe black hole and neutron star mergers as the detectors reach their design sensitivity. With many sources to observe, our group focuses both on ensuring that such observations happen and in exploring what science we can extract now that gravitational-wave astronomy is establishing itself as a brand-new tool for observing the Universe!
Observing compact binary mergers

Observing the signature of compact binary mergers buried within the data taken from large-scale gravitational-wave observatories is not a trivial task. The gravitational-wave signals that we see from such compact objects are faint and are often buried within the noise of the interferometric detectors. However, using highly accurate models of the gravitational-wave signals of compact binary mergers in matched filtering algorithms, we are able to extract possible signals from the noise. Matched filtering works by multiplying, for all times, the interferometer data by the expected gravitational-wave signal, weighting by the fact the detector is more sensitive at some frequencies than others, and then looking for any point where the resulting statistic produces a large value.
Constructing template banks
The gravitational-wave signals that Advanced LIGO and Advanced Virgo observe are dependent on the masses and spins of the compact objects being observed. Therefore matched-filtering with a binary-neutron star waveform is not able to observe a binary black hole merger. We must therefore construct a template bank of filters covering the full range of source parameters so as to be able to observe any potential compact binary merger in the data. Investigating and developing methods for constructing such template banks is one of the many areas we are working in.
Improving search sensitivity
As well as analysing the data taken by Advanced LIGO to observe gravitational-wave sources, we continue to study techniques to make these searches more sensitive, especially to certain astrophysically interesting configurations. For example, in cases where the spins of the component compact objects are not aligned with the orbital angular momentum the plane in which the system orbits can precess. In many configurations this is difficult to observe, but sometimes this precession is clearly observable in the gravitational-waveform, and this can greatly help when inferring the underlying physical parameters of the system. Unfortunately our current search techniques also have poor sensitivity to such systems. This is also true for systems with non-negligible eccentricity or where the sub-dominant gravitational-wave modes contribute strongly to the observed signal. We are working to try to develop new techniques to fill this gap in compact binary merger searches.

Pulsar timing arrays
We are also involved in the effort to detect gravitational-wave signals from observing pulsars in our Galaxy. Pulsars are often called the most precise clocks in the Universe because of the extreme regularity of their rotation and the pulses that we observe. Gravitational-waves passing by pulsars can shift these observed pulses by tiny amounts. Then, by observing many pulsars simultaneously in the Galaxy, we might hope to observe the long lived signals of orbiting compact objects many millenia before they would merge. European efforts towards gravitational-wave observation through pulsar timing occur through the EPTA (European Pulsar Timing Array) and IPTA (International Pulsar Timing Array) collaborations, both of which we are members of.
Extracting source parameters from gravitational-wave observations
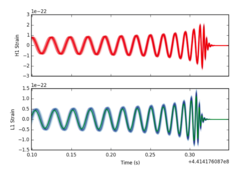
The other broad aim is to develop better methods for the extraction of physical information from compact binary mergers and to investigate how extracting this information informs our understanding of the formation and evolution processes of compact binary mergers. These measurement methods rely on a set of models of compact merger gravitational waveforms, developed and used in tight collaboration with the colleagues working on Source Modeling in the department. Such models are then combined with a model for the noise of the observatories to measure their quality of fit to the observed data. We use Bayesian statistical theory to report multidimensional probability density functions for the model parameters.
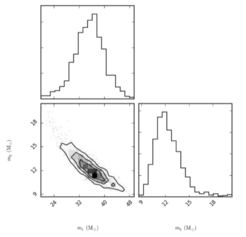
What is the recipe to obtain those probability density functions?
We start with a stretch of data to analyse, and assume a particular model for the gravitational-wave signal. That probability is computed by:
- choosing some parameters to compute the probability for
- computing the signal using the assumed model for those parameters
- subtracting this signal from the data
- calculating the probability of obtaining this particular residual by chance under a gaussian process following the instrument’s noise properties
- multiplying this value by the a priori assumption to obtain the a posteriori probability.
Step 1. is handled by Markov-Chain Monte-Carlo or Nested Sampling algorithms, which try to guess relevant values to use. Step 2. is in general the most computationally expensive, we compute Reduced Order Models for the most complex signal models. Step 4. can include additional noise modelling features, and step 5. parametrizes our understanding of gravitational-wave sources before the observation.
What can these observations teach us about the Universe?
When we accurately measure the various parameters that describe compact binary coalescences we can use this information to infer astrophysical formation mechanisms, and improve our understanding of stellar evolution. We also take advantage of the extreme settings that black-holes and neutron-stars provide to perform experiments that could not be done otherwise: we test Einstein’s theory of general relativity like never before, and with binary neutron stars and neutron star - black hole detections we will be able to measure the equation of state of matter at the highest densities physically possible.




