Theoretical Gravitational Dynamics and Radiation

For over a century Einstein's general relativity (GR) is our best description of gravity. On the one hand, it reduces to Newton's theory of gravity in the weak-field, slow-motion limit, and, thus, describes everyday gravitational physics on the earth and in the solar system – it also describes the tiny deviations from Newtonian gravity observed in precision tests in the solar system. On the other hand, GR makes exotic predictions in the regime of strong gravitational fields, such as the existence of black holes (BHs), and the fact that all orbiting bodies emit gravitational waves (GWs) which drive them to spiral into each other and (barring other influences) eventually merge together.

The existence of GWs has been proven through observations of binary pulsars within our Milky Way galaxy, which are seen to undergo orbital decay due to GW emission. However, these pulsars still move with velocities significantly smaller than the speed of light and they will not merge for hundreds of thousands of years.

Our first true tests of the exotic strong-field regime of GR for dynamical spacetimes came in 2015, with the first direct detections of GWs arriving at Earth by the Laser Interferometer Gravitational-Wave Observatory (LIGO). The first GW signal detected in 2015 seemed to have come from the inspiral and merger of two BHs. Since then multiple BBH mergers have been detected and in 2017 also the first binary neutron star merger was observed.

These detections mark the beginning of the age of GW astronomy. The analysis of the signals, thus far, has confirmed our expectations for the nature of GWs - but this is only the beginning of the science potential for LIGO and other GW observatories. The next stages of LIGO and Virgo promise significantly higher signal-to-noise ratios, translating into (i) more accurate tests of GR, and (ii) an increased number of detected signals. For binaries containing NSs, one must also consider the influence of the internal physics of the stars. Indeed, placing constraints on the cold supranuclear matter inside NSs is one of the main unsolved problems of modern nuclear physics. The first detection of a binary NS merger already placed constraints on the internal structure of the stars, but even tighter constraint will be possible with future detections over the next years.

Being able to detect GW signals and to extract science from them requires detailed models of the forms the signals might take. For binary BHs, this entails fleshing out the predictions of GR for the properties of BHs and binary dynamics and contemplating possible deviations from GR. For binaries containing NSs, one must also consider the influence of the still mysterious internal physics of NSs, in addition to applying all of the same techniques to solve Einstein's equations described below for the binary BH case.

Binary black holes

Black holes are regions of spacetime where matter has become so dense, after the collapse of a massive star, that gravity causes the matter to disappear behind an event horizon, a surface from which not even light can escape and near which time almost stands still. While astronomers have found numerous candidate dense objects that fit the description, a concrete demonstration that BHs exist precisely as predicted by GR remains elusive. 

The binary-BH-merger GW detections have greatly increased our confidence in our understanding of BHs and GR, but their relatively modest signal-to-noise ratios leave many open questions to be addressed with future observations.  As with the first observations, GW science requires us to anticipate and parametrize the detailed forms of GW signals from merging binaries, so that we can recognize and interpret them once they arrive.

For the case of two BHs in a binary, GR alone provides definite predictions for the orbit and the GW signal, and we should thus already know what we're looking for – if we can solve Einstein's equations. However, finding a sufficiently accurate, general, and practical solution to the relativistic two-body problem has proved notoriously difficult, and currently occupies many physicists around the world and in our department at the AEI.

Solving the relativistic two-body problem

The field of numerical relativity uses supercomputing power to directly solve Einstein's equations, and has found great success in determining the evolution of nearly-equal-mass binary BHs. But it remains difficult to cover the entire parameter space (of the BHs' initial masses, spins, and orbital parameters), since a simulation for a given set of parameters can take months, and since simulations still struggle to reach into extreme parts of the parameter space. Successful models of GWs from binary BHs will have to incorporate both data from numerical relativity and analytic approximations to GR.

The two-body problem lends itself to two complimentary lines of attack by analytic means, which are valid in two limiting regions of the parameter space: In the limit of weak gravity and slow motion, GR reduces to Newtonian gravity; expanding about this limit yields the post-Newtonian (PN) approximation. In the limit where one BH is much larger than the other, the problem reduces to a test-mass following a geodesic in the stationary spacetime of the large BH; expanding about this limit yields the extreme-mass-ratio (EMR) approximation. The effective-one-body (EOB) formalism incorporates information from the PN limit, the EMR limit, and numerical relativity in attempt to provide an accurate model throughout the parameter space.

The post-Newtonian approximation

Post-Newtonian (PN) theory is a systematic perturbative approximation to General Relativity valid in weak-field, slow-motion situations. It was first developed in the 1920s and 30s, and has been iterated to high orders for point-masses. The PN results have enabled exquisite tests of relativistic effects in the solar system and binary pulsars. However, the PN description of physical effects at higher order, such as those due to the bodies’ spins, remains incomplete. Members of the ACR department are working on advancing the knowledge of spin effects in PN theory using a variety of approaches which serve as independent cross checks:  (i) a formulation in harmonic gauge in which the solutions of the PN equations are calculated directly, iterating between the solutions for the motion and for the gravitational field, (ii) a Hamiltonian framework for the conservative sector, and (iii) methods adapted from effective field theory for the conservative dynamics, where the problem is cast into Feynman diagrams that can be efficiently computed and power counting methods can be used to readily identify relevant contributions at each PN order. The researchers use computer algebra packages to make their calculations tractable, although much work is also done purely analytically. The results of this effort have led to new insights into the behaviour of the spins and angular momentum during a binary inspiral and substantially improved the modeling of physically realistic binaries.  

The extreme-mass-ratio approximation

In the EMR approximation, the zeroth-order solution is given by a test-particle moving along a geodesic of a background black hole spacetime – the Schwarzschild spacetime of a non-spinning black hole or the Kerr spacetime of a spinning black hole. Corrections to this solution come both from "finite-size" effects on the small body's motion, due to its spin and its intrinsic and tidally induced deformations, and to "self-force" effects, arising from the back-reaction of the small body's perturbation to the gravitational field. Computing self-force effects on binary motion is a relatively nascent yet active field of study, which combines analytical and numerical techniques. Understanding the two-body problem in the EMR limit will be crucial for the analysis of gravitational waves from inspirals of stellar-mass objects into supermassive BHs detected by future space-based detectors like LISA, as well as for developing models which can describe the entire parameter space.

The effective-one-body description

The EOB formalism is a synergistic approach to the two-body problem which incorporates information from the PN limit, the EMR limit, and numerical relativity in an attempt to provide an accurate effective description of binary motion throughout the parameter space. The core idea of the EOB model is to recover exact strong-field results from the spinning test-mass limit in the Kerr spacetime while incorporating all known results from PN theory for finite mass ratios through a carefully chosen deformation of the Kerr spacetime. The conservative dynamics is described by a Hamiltonian, which is then supplemented by radiation reaction forces coupled with generation of wave modes. The model is flexible enough to be calibrated to data from numerical relativity, and provides complete waveforms for the inspiral, the merger, and the ringdown of the remnant BH.

Neutron star binaries

Neutron stars (NSs) represent the most extreme gravitational, electromagnetic and nuclear physics environments that stably exist in the universe. They are formed when the degenerate cores of massive stars collapse in a supernova explosion. Several thousands of NSs have been observed to date; they have masses comparable to the sun’s but with all the matter compressed into a sphere with a radius of merely around 10km, spinning with up to 38000 rpm, and with magnetic fields up to a hundred trillion times stronger than the Earth’s field. The densities in NS interiors are so high that they reach well above the mean density of an atomic nucleus. At such extreme densities, the structure of nuclear matter known from fundamental physics completely disintegrates and instead new, exotic phases of matter may emerge. Determining the properties of such ultra-dense matter such as its composition and equation of state has been a longstanding science goal both in fundamental physics and astrophysics.

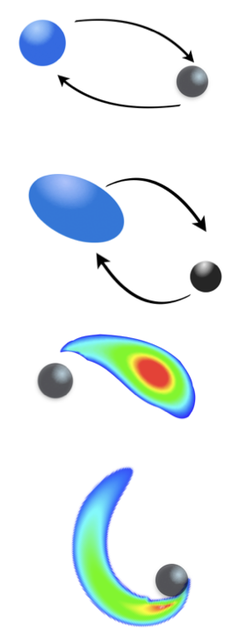
Key insights into neutron star interiors can be obtained from the gravitational waves from a neutron star binary inspiral. The success of extracting this information, however, relies on a detailed understanding of the effects of the neutron star matter on the dynamics and gravitational wave emission. As the two objects approach each other, the NS begins to respond to the tidal field due to the companion and deforms, similar to the tidal bulges raised on the earth by the moon’s differential gravity. For a NS-BH binary, the inspiral terminates either when the NS plunges into the BH or when the BH’s tidal force becomes stronger than the NS’s self-gravity and tears apart the NS material which then spreads out into a tidal tail. For NS-NS binaries on the other hand, the merger is dominated by hydrodynamics. The details of these processes and the identification of characteristic parameters linking the GW signal to the NS matter remain still need more exploration.

Members of the ACR department advance this knowledge by using the same analytical techniques as described for black hole binaries, augmenting them with additional calculations describing the complexities of matter. For example, we compute the response of the NS's internal structure to an external tidal field in perturbation theory for various models of neutron star interiors. Since NSs are strongly self-gravitating objects this must be done in fully relativistic framework. These calculations provide a direct link between the NS microphysics and its global properties such as the tidally induced multipole moments. To describe how the NS structure influences the two-body dynamics, researchers in the ACR department develop the theory of tidal interactions within the PN framework, using additional insights on the strong field physics in the test particle limit. Furthermore, they formulate and test non-perturbative re-summations of these results in the EOB framework to extend the model up to the merger. An important aspect of the work is to devise predictions for the characteristic parameters that encode the influence of the NS matter on the GWs.

Questions addressed by the theoretical work in the department:

• What are efficient strategies to advance the knowledge of the two-body problem in General Relativity and to include more physical effects?
• What is the effect of the black holes' absorption of GWs?
• What are observable features due to the  black holes' spins, when they interact mutually and with the orbital angular momentum?
• How does the richer character of non-circular motion manifest in the GWs?
• How does the NS respond to the companion’s tidal field?
• What is the effect of the tidally perturbed NS structure on the two-body dynamics?
• What are the key parameters characterizing the imprint of the NS matter in the GWs?
• For NS-BH binaries, what underlying physics determines the frequency of tidal disruption?
• For NS-NS binaries, do nonlinearities become important near the merger?